CONJETURAS Y PRUEBAS EN MATEMÁTICAS

3. TRABAJANDO CON CONJETURAS Y TRATANDO DE PROBARLAS
Conjetura: Todo cubo es diferencia de dos cuadrados.
Proposición 1. La suma de los impares consecutivos empezando en 1 es un cuadrado.

ESTUDIO DE LOS INDICIOS

1+ 3 = 22 = 4

1+ 3 +5 = 32 = 9

1+ 3 +5 +7 = 42 = 16

1+ 3 +5 +7 +9 = 52 = 25

1+ 3 +5 +7 +9 +11 = 62 = 36

1+ 3 +5 +7 +9 +11+13 = 72 = 49

................................

Demostraciones:
a) Por la suma de las progresiones aritméticas
S = 1 + 3 + 5 + 7 + · · · + 2n–1

S = 2n-1 + 2n-3 + 2n-5 + 2n-7 + · · · + 1

2S = 2n + 2n + 2n + 2n + + 2n = n · 2n = 2n²
Luego S = n².
b) Más elegante era la demostración geométrica griega que la realizaban interpretando las orlas de un cuadrado

Observacion de Nicómaco de Gerasa (Siglo I) sobre las sumas parciales de los números impares:
 

1+ 3 +5 +7 + 9 + 11+ 13 +15 + 17 + 19 + 21 + 23 + 25 + 27 + 29 + ···

1       8              27                        64                                     125

¿Es casualidad o se deja de cumplir para valores grandes?
Si la observación
de Nicómaco fuera verdadera para todos los valores podríamos afirmar que la conjetura propuesta es verdadera y que cada cubo es difresncia de dos cuadrados.
Lo que observó Nicómaco es que, comenzando por el 1, haciendo grupos de impares consecutivos de uno, dos, tres, cuatro elementos la suma de cada uno de los grupos (que llamaremos suma de grupos de Nicómaco) resulta ser un cubo.
Para hacer la demostración tendremos que probar lo siguiente:
1) La suma del grupo n-ésimo de Nicómaco será n³.
Para ello tendremos en cuenta una serie de observaciones
2) El grupo n-ésimo de Nicómaco tiene delante 1+2+3+ ··· +(n-1) impares consecutivos.
3) El número de orden del primer elemento del grupo n-ésimo, del grupo cuya suma es n³ será 1+2+3+ ··· +(n-1) +1
1+2+3+ ··· +(n-1) +1= = =
4) El primer término del grupo será 2 =
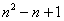
5) Los elementos que están en el grupo n de Nicomaco serán:
, , , ···
6) Su suma será.
=
Que es lo que deseábamos probar.