..........Geometría.........

Introducción

1. Reseña histórica.
2. Geometría
3. Euclides
4. Los Elementos de Euclides
5. Reseña Histórica de la Evolución de las Geometrías no Euclideanas
6. Geometría de Lobatchevsky
7. El significado Real de la Geometría de Lobatchevsky
8. Conclusión
9. Anexos
10. Bibliografía

Bibliografía ................(Geometría)

• Dowmns, Moise. Geometría Moderna. Addison-Wesley Iberoamericana
• Wentworth, J., Smith, D. E. Geometría Plana y del Espacio. Editorial Porrúa
• Landaverde, J. Curso de Geometría. Editorial Progreso.
• Thompson, A. Geometría al alcance de todos. Editorial UTHEA.

• Fetisov, A. I. Acerca de  la demostración. Editorial MIR.

• Piaget, J., Inhelder, B. and Szeminska, A. The Child's conception of geometry. Prentice Hall.

• http://es.geocities.com/eucliteam/ fecha(13/08/04)

• http://centros5.pntic.mec.es/ies.ortega.y.rubio/Mathis/Euclides/euclides.htm fecha(13/08/04)
• http://www.terra.es/personal/jftjft/Historia/Biografias/Euclides.htm fecha(13/08/04)
• http://euler.ciens.ucv.ve/matematicos/euclides.html fecha(13/08/04)
• http://www.arrakis.es/~mcj/euclides.htm fecha(13/08/04)
• http://www.xtec.es/~jdomen28/indiceeuclides.htm fecha(13/08/04)
• http://www.oya-es.net/reportajes/euclides.htm fecha(13/08/04)
• http://www.mat.usach.cl/histmat/html/alexandr.html fecha(13/08/04)
• http://www.biografiasyvidas.com/biografia/e/euclides.htm fecha(13/08/04)
• http://mural.uv.es/beaco/tr4.htm fecha(11/09/04)
• http://www.domos.cl/geomatem.htm fecha(11/09/04)
• http://mural.uv.es/beaco/tr2.htm fecha(11/09/04)
• http://mural.uv.es/beaco/tr1.htm fecha(11/09/04)

[1] Ver Anexos

[2] Ver Anexos

[3] Ver Anexos

Anexos ....................(Geometría)

GAUSS, Carl F. (1777-1855): Matemático alemán nacido en Brunswick y fallecido en Gotinga. Gauss fue un niño prodigio en matemáticas y continuó siéndolo toda su vida. Hay quien le considera uno de los tres mayores matemáticos de la historia junto a Arquímedes y Newton. Su inteligencia superdotada llamó la atención del duque de Brunswick, quien decidió costearle todos sus estudios, entrando en 1795 en la universidad de Gotinga. Antes de cumplir los veinte años hizo algunos descubrimientos importantes, entre los que se incluye el método de los mínimos cuadrados. Gauss halló un método para construir un polígono equilátero de 17 lados con ayuda de regla y compás, e incluso fue más allá, demostrando que sólo ciertos polígonos equiláteros se podían construir con ayuda de regla y compás. Hizo una labor importante en la Teoría de Números. También construyó una geometría no euclídea, basada en axiomas distintos a los de Euclides, pero se negó a publicarla. Lovachevski y Bolyai ostentan el honor de su descubrimiento al publicarla algo más tarde. En 1799 Gauss demostró el teorema fundamental del álgebra. También demostró que los números se podían representar mediante puntos en un plano. El 1801 demostró el teorema fundamental de la aritmética. Se levantó una estatua en su honor en su ciudad natal, que descansa sobre un pedestal en forma de estrella de 17 puntas, en celebración de su descubrimiento de la construcción del polígono de 17 lados. Le llamaban Príncipe de las Matemáticas.

BOLYAI, Janos (1802-1860): Matemático húngaro nacido en Kolozsvar y fallecido en Marosvásárheli, ambas en Hungría. Su padre había sido gran amigo de Gauss, llegando incluso a intentar demostrar el quinto axioma de Euclides. En 1825 ponía en práctica los mismos proyectos que Lovachevski sobre la geometría no euclideana, publicando en 1831 un apéndice en un libro de su padre sobre matemáticas. En él explicó su geometría, que Lovachevski había publicado tres años antes.

SACCHERI, Giovanni Girolamo (1667-1733): Nació y murió en San Remo, Génova (ahora Italia). Se unió a la Orden de los Jesuitas en 1865. Cinco años después marchó a Milán, donde estudió filosofía y teología en el Colegio Jesuita. Allí, Tommaso Ceva le animó a estudiar matemáticas. En 1694 fue ordenado sacerdote y se dedicó a enseñar en colegios jesuitas. Fue catedrático de matemáticas en Pavia desde 1699 hasta su muerte

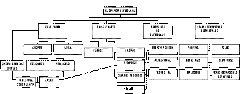
Esquema de la evolución de la Geometría no Euclidianas

Conclusión ..............(Geometría)

Gracias a la realización de este trabajo pudimos comprender un poco mejor lo que es la geometría Euclídea; las repercusiones que ésta tuvo en pensamiento del mundo antiguo.

Además de conocer las diferencias que existen entre los distintos tipos de geometría, y de los pensadores responsables de sus fundaciones, es muy interesante reconocer y estudiar estas diferencias, ya que nos muestran las diversas formas de pensamiento de la mente humana.

El estudio formal de la geometría euclidiana y de las demás geometrías nos permite organizarlas de forma tal que podemos conocer y entender sus estructuras conceptuales, facilitando así su estudio futuro.

El estudio de los Elementos de Euclides es muy importante ya que es la recopilación de todos sus pensamientos e ideales, además de contar con todos sus axiomas, postulados y teoremas, los cuales son de gran utilidad para entender y poder aplicar su concepto de geometría.

Estructura conceptual de la Geometría.

El significado Real de la Geometría de Lobatchevsky

Eugenio Beltrami

Biografía

  En 1868 el italiano Eugenio Beltrami publicó Ensayo sobre la interpretación de la Geometría no euclídea, que proporcionó un modelo para la geometría no-euclidiana de Lobatchevsky dentro de la geometría euclídea 3-dimensional.

Fotografía de Beltrami

Obra

Consideró una curva llamada tractriz (ver FIGURA 5). Una de las propiedades de esta curva es que la longitud del segmento de tangente comprendido entre el punto de tangencia y el punto de corte con el eje OY es constante. El eje OY es una asíntota. Al girar la curva alrededor de su asíntota se engendra una superficie llamada seudoesfera, representada en la parte derecha de la FIGURA 5.

FIGURA 5: Tractriz y seudoesfera

Beltrami hizo notar que la geometría intrínseca de la seudoesfera coincide con la geometría sobre parte del plano de Lobatchevsky. De este modo, esta geometría no euclidiana tiene un perfecto significado real: no es más que una exposición abstracta de la geometría sobre la seudoesfera.

         Pero, como hemos mencionado con anterioridad, Beltrami sólo estableció una correspondencia entre la seudoesfera y parte del plano de Lobatchevsky. El problema de dar