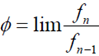Hoy una vez más hablare sobre otra curiosidad de la serie de Fibonacci. En esta ocasión solo mostraré la relación que tiene con el triángulo de Pascal (también conocido como triángulo de Tartaglia), el mismo que da los coeficientes en la expansión de un binomio.
En principio estos dos objetos matemáticos no tienen demasiada relación. Pero en realidad sí la tienen. La sucesión de Fibonacci aparece en multitud de lugares, tanto matemáticos como reales. Y el triángulo de Pascal no iba a ser una excepción. ¿Cómo encontrar los elementos de la sucesión de Fibonacci en el triángulo de Pascal?. Pues de esta forma:
Cada uno de los términos de la sucesión de Fibonacci se obtienen, como luego se comprobaría, sumando las diagonales del Triangulo de Tartaglia, tal como indicamos en la figura:

Es decir,