Este post esta dedicado para un chavo de nuestros lectores que a través de la pagina de Facebook nos pidió este tema. Las operaciones que se realizaran son simplemente algebraicos. Espero que les guste y gracias por la espera.
Usando el número áureo es posible deducir una fórmula que permite obtener el término general de la sucesión, para todo valor n. Esto hace posible que se pueda calcular un término cualquiera de la sucesión de Fibonacci sin necesidad de calcular todos los términos anteriores. La fórmula que nos facilita esto es la expresión de Binet-Moivre: Demostración:
Demostración:
 Demostración:
Demostración:
Análogamente la sección áurea,
eligiendo los coeficientes a y b de forma que se verifiquen las condiciones de definición de la sucesión de Fibonacci:
Fuentes:
- Huntley, H.E.; The divine proportion, Dover Publications, Inc., 1970, Nueva York


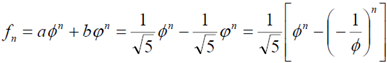


No hay comentarios.:
Publicar un comentario