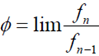Historia de las matemáticas IV (Hacía el infinito y más allá)

En mayo de 1831 asistimos al descubrimiento y pérdida de un genio matemático: antes de morir en un duelo combatiendo por su amante, Evariste Galois había trazado un teorema que con el tiempo despejaría los misterios de la simetría. En Rusia, George Cantor descubrió no sólo que el infinito existe, sino que llegó a demostrar que hay dos tipos de infinito. El ordenador revolucionó las matemáticas al permitir realizar cálculos a una velocidad de vértigo ayudando a los matemáticos a "contemplar" el caos, pero los resultados sin comprender sus procesos siguieron desconcertando a los matemáticos. Muchos sostienen que el placer de las matemáticas se encuentra en la comprensión del problema, no sólo en su correcta solución. En 1900, el matemático francés David Hilbert enumeró los principales misterios matemáticos sin resolver, trazando así el camino que seguirían las matemáticas durante el siglo XX. 15 de estos 23 problemas ya han sido resueltos parcial o totalmente, aún se sigue trabajando en el resto...



Parte 3

Historia de las matemáticas III (Las fronteras del espacio)

En el siglo XVI, los problemas matemáticos se convirtieron en un espectáculo de masas con grandes premios para los ganadores. En este ambiente tan competitivo, no es de extrañar que los matemáticos guardaran celosamente sus conocimientos y que, en algunos casos, se portaran muy mal. Girolamo Cardano parecía haber resuelto una ecuación cúbica, pero había robado la solución de un matemático rival, Nicolo Tartaglia. Francia comenzó a retar el dominio italiano sobre las matemáticas con Rene Descartes, que unificó el álgebra y la geometría, un paso decisivo que cambiaría el curso de esta disciplina para siempre. Le siguió el prodigioso matemático Pascal, quien con tan sólo 12 años, logró demostrar que los ángulos de un triangulo suman dos ángulos rectos. Más tarde el mismo Pascal inventaría una calculadora mecánica y demostró la existencia del vacío. En Inglaterra, Isaac Newton desarrolló una formula capaz de explicar las órbitas de los planetas, aunque pasaría el resto de su vida embrollado en una disputa con un matemático alemán sobre quién lo había desarrollado primero...

Parte 2                                                             Parte 4

Historia de las matemáticas II (El genio del este)

Los Mayas concibieron un calendario increíblemente preciso. Su cálculo del mes lunar varía sólo 0,0004 del valor del día aceptado por los astrónomos actualmente.

Este documental muestra que alrededor del año 200 a.C., en China, la dinastía Han encargó a los sabios la recopilación de un libro conocido como "Los nueve capítulos" donde pretendieron recuperar y preservar para siempre las enseñanzas entonces perdidas de los antiguos matemáticos chinos. El texto se destinó a solucionar problemas prácticos del mundo real: cómo dividir terrenos y bienes o cómo calcular obras de construcción. India fue la primera civilización en desarrollar un sistema numérico que incluía un símbolo especial para representar el cero- uno de los mayores hitos en el desarrollo de las matemáticas. Aryabhata [476-550 d.C.] elaboró una fórmula para encontrar el número Pi que calcula su valor real de forma más precisa que cualquier otro método contemporáneo. En el siglo VII d.C. un nuevo califato se estableció en Bagdad, aspirando a convertirse en el mayor foco intelectual del mundo. Fundaron un nuevo centro de estudios llamado "La casa del saber", que se convertiría en el centro de los intentos por aunar todos los conocimientos matemáticos de Grecia, India y Babilonia..., y como siempre digo espero les guste.
Parte 1                                                                           Parte 3

Historia de las matemáticas I (El idioma del Universo)

Las matemáticas o la matemática (del lat. mathematĭca, y este del gr. μαθηματικά, derivado de μάθημα, conocimiento) es una ciencia formal que, partiendo de axiomas y siguiendo el razonamiento lógico, estudia las propiedades y relaciones entre entidades abstractas (números, figuras geométricas, símbolos).

La historia de las matemáticas es el área de estudio que abarca las investigaciones sobre los orígenes de los descubrimientos en matemáticas, de los métodos matemáticos, de la evolución de sus conceptos y también en cierto grado, de los matemáticos involucrados. Sin las matemáticas, no tendríamos ni arquitectura, ni comercio, ni hora, ni química. La medición del tiempo dio origen a los instrumentos matemáticos más antiguos del mundo. Los primeros sistemas matemáticos completos se desarrollaron en Babilonia, Egipto y Grecia.

Un profesor de matemáticas de la Universidad de Oxford investiga la historia de las matemáticas, que abarca más de 30.000 años, y ofrece explicaciones claras y accesibles sobre el desarrollo de los principios matemáticos clave que forman la base de la ciencia, la tecnología y la cultura de nuestro mundo moderno, disfruten el documental....


Parte 2 

El tramposo de las Maquinas

Como ya les debo varios post hoy les traigo un documental muy curioso acerca de un personaje que utilizo su astucia para hacer de las suyas espero les guste.
Tommy Glenn Carmichael había nacido en 1950. Él es considerado como uno de los mayores tramposo de la historia de Las Vegas. Todo comenzó en 1980, cuando Carmichael encontró con un amigo Ray Ming, quien le mostró una máquina tragaperras. 

Este documental nos narra la vida de este ladrón de maquinas traga monedas que logró amasar una gran fortuna haciendo trampas para quedarse fácilmente con el dinero de todas las maquinas tragamonedas. Electricista de profesión, un día decidió dejarlo todo y dedicarse a robar maquinas traga monedas en Las Vegas. Es un reportaje muy interesante, espero que lo veáis.

¿Qué les pareció?

Relación entre el triángulo de Pascal y la sucesión de Fibonacci

Hoy una vez más hablare sobre otra curiosidad de la serie de Fibonacci. En esta ocasión solo mostraré la relación que tiene con el triángulo de Pascal (también conocido como triángulo de Tartaglia), el mismo que da los coeficientes en la expansión de un binomio. 

En principio estos dos objetos matemáticos no tienen demasiada relación. Pero en realidad sí la tienen. La sucesión de Fibonacci aparece en multitud de lugares, tanto matemáticos como reales. Y el triángulo de Pascal no iba a ser una excepción. ¿Cómo encontrar los elementos de la sucesión de Fibonacci en el triángulo de Pascal?. Pues de esta forma: 

Cada uno de los términos de la sucesión de Fibonacci se obtienen, como luego se comprobaría, sumando las diagonales del Triangulo de Tartaglia, tal como indicamos en la figura:

Es decir,

Obtención del número de oro desde la sucesión de Fibonacci:

Hemos estado abordando algunas curiosidades de la sucesión de Fibonacci, en el post anterior abordamos como obtener el termino general de esta serie a partir del numero de oro, ahora haremos lo opuesto obtendremos el numero de oro desde la sucesión de Fibonacci.

Es necesario mencionar que en todas las ocasiones que mencione el limite se referirá al que por cuestiones practicas no coloque.

El cociente de dos términos consecutivos de la sucesión de Fibonacci, f_{n +1}/f_n , se aproxima al número de oro cuando el orden de los términos crece indefinidamente:

Demostración: 

Por construcción de la sucesión es f_n=f_n−1+f_n−2. Dividiendo ambos miembros por f_{n −1} será:   

 

Llamando    , se tiene:, o sea, , ecuación de segundo grado cuya única raíz válida es

Luego se verifica que 

Fuentes:

- Huntley, H.E.; The divine proportion, Dover Publications, Inc., 1970, Nueva York

- http://casanchi.com/

Obtención del término general de la sucesión de Fibonacci desde el número de oro

Este post esta dedicado para un chavo de nuestros lectores que a través de la pagina de Facebook nos pidió este tema. Las operaciones que se realizaran son simplemente algebraicos. Espero que les guste y gracias por la espera.

Usando el número áureo es posible deducir una fórmula que permite obtener el término general de la sucesión, para todo valor n. Esto hace posible que se pueda calcular un término cualquiera de la sucesión de Fibonacci sin necesidad de calcular todos los términos anteriores. La fórmula que nos facilita esto es la expresión de Binet-Moivre:Demostración:

De ser , si multiplicamos toda la expresión por , es decir, satisface la sucesión de Fibonacci.

Análogamente la sección áurea,

y como son del mismo signo los términos se tendrá: 

y, multiplicando ahora toda la expresión por:

Razón de oro

 Este post es para que mas adelante podamos entender una propiedad la sucesión de Fibonacci, hablaremos de un numero muy interesante.
El número áureo o de oro (también llamado razón extrema y media, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) representado por la letra griega φ (fi) (en minúscula) o Φ (fi)
Aparece muchas veces en geometría, arte, arquitectura y otras áreas.

La idea

Si divides una línea en dos partes de manera que:
la parte larga dividida entre la corta
es igual que
el total dividido entre la parte larga
entonces tienes la razón de oro.

De hecho el valor exacto es:

1,61803398874989484820... (continúa sin repetirse)
Las cifras siguen sin repetirse. De hecho se sabe que la razón de oro es un número irracional, y hablaremos sobre eso más adelante.

Calcularlo

Puedes calcularlo tú mismo empezando por

Si hay pobreza ¿Por qué no fabricamos más dinero?

Éste post lo escribo en especial para una persona que me dijo lo siguiente "Si hay pobreza ¿Por qué no fabricamos más dinero?", a mi parecer una pregunta muy interesante. El razonamiento en principio parece lógico, puesto que si la gente no tiene dinero, al estado no le costaría mucho imprimir unos cuantos billetes para entregarle a cada persona, lo que supondría una solución a la pobreza.

El problema es que la economía no funciona así. La solución a la pobreza es mucho más complicada que “soplar y hacer billetes”.

También sucede que mucha gente tiene la idea errónea de que la cantidad de dinero que circula en un país esta respaldada por la cantidad de oro que posee. Sin embargo, esto simplemente no es cierto – cualquier país puede imprimir tanto dinero como desee – y no necesita de ninguna cantidad de oro para respaldarlo.

Se considera que el valor del dinero debería

ALCANOS

Estructura electrónica del Carbono.
El átomo de carbono posee un total de seis electrones, los que están dispuestos en diferentes orbitales atómicos, como se muestra en el diagrama de energías:

Diagrama Nº1

Los alcanos y la hibridación sp³.
Cuando el átomo de carbono va a formar parte de una molécula utilizando su saturación máxima, uno de los electrones del orbital atómico 2s, salta al orbital 2pz que está vacío. Este salto tiene por supuesto un costo en energía, el cual es compensado sobradamente con la energía que es liberada al formar el enlace entre uno de estos nuevos orbitales híbridos sp³ del carbono y el orbital del otro átomo. Por ejemplo C-C o C-H. Así, todos los orbitales del nivel 2 quedan con un electrón cada uno. Y en ese momento al combinarse entre sí, dan origen a cuatro orbitales híbridos.

Diagrama Nº2
Estos 4 orbitales sp³ tienen un electrón cada uno, son equivalentes en